Methods for Converting Between Different Number Bases
What is Base Conversion
Base conversion is the process of converting a number from one counting and carry rule to another, with the core being to maintain the actual value of the number while only changing its representation form.
Key Points
- Common number bases include decimal (used in daily life, carries over when reaching 10), binary (used in computers, carries over when reaching 2), octal (carries over when reaching 8), and hexadecimal (carries over when reaching 16).
- The core logic of conversion is “value equivalence”. For example, the decimal number “5” is represented as “101” in binary; both essentially represent the same value.
- Just like the same amount of money can be converted into “yuan, jiao, fen” (Chinese currency units) or “dollars, cents”, the amount itself remains unchanged, only the counting units and carry rules change.
- Conversions are divided into “forward conversion” (decimal to other bases) and “reverse conversion” (other bases to decimal), each with fixed calculation methods.
Base Conversion Methods: Sum-of-Weights Expansion Method, Division-by-Base and Remainder-Taking Method
- The sum-of-weights expansion method is used for converting non-decimal bases to decimal.
- The division-by-base and remainder-taking method is used for converting decimal to non-decimal bases.
Sum-of-Weights Expansion Method (Non-decimal → Decimal)
Core Principle
Any number in a given base is essentially the sum of “each digit × the weight of its position”. The weight of a position follows the rule: it is the power of the base of the target system, with the position index (counting from right to left, starting at 0) as the exponent. For example, in binary (base 2), the weight of the 1st position from the right (the rightmost) is \(2^0 = 1\), the 2nd position is \(2^1 = 2\), the 3rd position is \(2^2 = 4\), and so on.
Steps
- Identify each digit of the number to be converted and the corresponding “weight value” of its position (weight value = base^position index, where the position index starts at 0 and counts from right to left).
- Multiply each digit by its corresponding weight value to get the decimal value of that position.
- Sum the decimal values of all positions; the result is the final decimal number.
Examples
- Binary: \(1001_{(2)} = 1 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 = 8 + 0 + 0 + 1 = 9_{(10)}\)
- Octal: \(302_{(8)} = 3 \times 8^2 + 0 \times 8^1 + 2 \times 8^0 = 192 + 0 + 2 = 194_{(10)}\)
- Hexadecimal: \(EA7_{(16)} = 14 \times 16^2 + 10 \times 16^1 + 7 \times 16^0 = 3751_{(10)}\)
Division-by-Base and Remainder-Taking Method (Decimal → Non-decimal)
Core Principle
A decimal number can be decomposed into the sum of powers of the base of the target system. By “dividing by the base and taking the remainder”, we can find each digit from the least significant bit to the most significant bit in sequence. Finally, reversing the order of the remainders gives the number in the target base. Simply put: the remainder is the “lower bit”, and continuing to divide the quotient is to find the “higher bit”.
Steps
- Divide the decimal number by the base of the target system to get a quotient and a remainder.
- Continue dividing the quotient from the previous step by the base, repeating the process to get a new quotient and remainder.
- Stop when the quotient is 0. Arrange all remainders in the order of “last obtained first placed” to get the number in the target base.
Example

Correspondence Between the First 17 Decimal Integers and Their Binary, Octal, and Hexadecimal Equivalents
| Decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Binary | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | 10000 |
| Octal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 20 |
| Hexadecimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 |
Conversion Between Binary and Octal/Hexadecimal
- Binary to octal is grouped by 3 bits; binary to hexadecimal is grouped by 4 bits.
- Reverse conversion involves splitting and padding with zeros: if the number of bits is insufficient, pad with zeros at the high position.
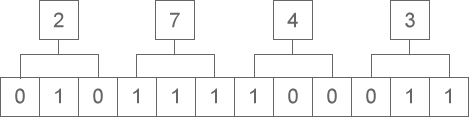
Binary to Octal (2→8)
- Start from the right end of the binary number and group every 3 bits.
- If the leftmost group has fewer than 3 bits, pad with zeros in front to make 3 bits.
- Each group corresponds to an octal digit (0-7); combining these digits gives the octal number.
Binary to Hexadecimal (2→16)
- Start from the right end of the binary number and group every 4 bits.
- If the leftmost group has fewer than 4 bits, pad with zeros in front to make 4 bits.
- Each group corresponds to a hexadecimal digit (0-9, A-F); combining these digits gives the hexadecimal number.

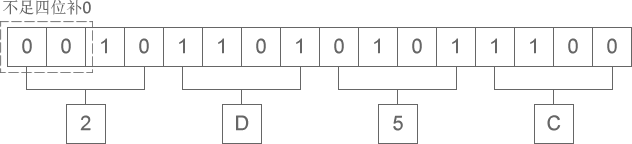
Octal / Hexadecimal to Binary (8/16→2)
- Octal to binary: Each octal digit is split into a 3-bit binary number (pad with zeros in front if fewer than 3 bits).
- Hexadecimal to binary: Each hexadecimal digit is split into a 4-bit binary number (pad with zeros in front if fewer than 4 bits).
- Remove any extra zeros at the leftmost end of the combined result (if any) to get the binary number.
Conversion of Fractional Numbers
- Decimal → other bases: For the integer part, use “division-by-base and remainder-taking, reverse order arrangement”; for the fractional part, use “multiplication-by-base and integer-taking, sequential arrangement”; finally, concatenate the two parts.
- Other bases → decimal: Both the integer part and the fractional part use the “sum-of-weights expansion” method, then combine the results.
Decimal to Other Bases
Integer Part: Division-by-Base and Remainder-Taking, Reverse Order Arrangement
- Steps: Divide the decimal integer by the base R, record the remainder; continue dividing the quotient by R until the quotient is 0; finally, arrange all remainders from last to first to get the integer part in base R.
- Example: Convert decimal 10 to binary (R=2)
- \(10 \div 2 = 5\), remainder 0;
- \(5 \div 2 = 2\), remainder 1;
- \(2 \div 2 = 1\), remainder 0;
- \(1 \div 2 = 0\), remainder 1;
- Reverse the remainders: 1010, i.e., \(10_{(10)} = 1010_{(2)}\).
Fractional Part: Multiplication-by-Base and Integer-Taking, Sequential Arrangement
- Steps: Multiply the decimal fraction by the base R, record the integer part (0 or 1 when R=2); continue multiplying the remaining fractional part by R until the fractional part is 0 or the required precision is reached; finally, arrange the integer parts in sequence to get the fractional part in base R.
- Example: Convert decimal 0.25 to binary (R=2)
- \(0.25 \times 2 = 0.5\), integer part 0;
- \(0.5 \times 2 = 1.0\), integer part 1;
- The fractional part is 0, stop;
- Arrange the integers in sequence: 01, i.e., \(0.25_{(10)} = 0.01_{(2)}\).
Other Bases to Decimal
Integer Part: Weights are \(R^0\), \(R^1\), \(R^2\)… (from right to left)
- Steps: Multiply each digit of the integer in base R by its corresponding weight, then sum the results.
- Example: Convert binary 1010 to decimal (R=2)
- Digit values from right to left: 1st digit 0 (weight \(2^0\)), 2nd digit 1 (weight \(2^1\)), 3rd digit 0 (weight \(2^2\)), 4th digit 1 (weight \(2^3\));
- Calculation: \(1\times 2^3 + 0\times 2^2 + 1\times 2^1 + 0\times 2^0 = 8+0+2+0 = 10\).
Fractional Part: Weights are \(R^{-1}\), \(R^{-2}\), \(R^{-3}\)… (from left to right)
- Steps: Multiply each digit of the fraction in base R by its corresponding weight, then sum the results.
- Example: Convert binary 0.01 to decimal (R=2)
- Digit values from left to right: 1st digit 0 (weight \(2^{-1}\)), 2nd digit 1 (weight \(2^{-2}\));
- Calculation: \(0\times 2^{-1} + 1\times 2^{-2} = 0+0.25 = 0.25\).