Metode Konversi Sistem Bilangan yang Berbeda
Apa itu Konversi Sistem Bilangan
Konversi sistem bilangan adalah proses mengubah angka dari satu aturan pembulatan penghitungan ke aturan lainnya, dengan inti mempertahankan nilai aktual angka tetap sama, hanya mengubah bentuk representasinya.
Poin Penting
- Sistem bilangan umum termasuk desimal (digunakan sehari-hari, penuh 10 naik 1), biner (digunakan komputer, penuh 2 naik 1), oktal (penuh 8 naik 1), heksadesimal (penuh 16 naik 1).
- Logika inti konversi adalah “kesetaraan nilai”, misalnya “5” dalam desimal, direpresentasikan sebagai “101” dalam biner, keduanya pada dasarnya adalah nilai yang sama.
- Seperti jumlah uang yang sama, dapat diubah menjadi “yuan, jiao, fen”, juga dapat diubah menjadi “dolar, sen”, jumlah uang itu sendiri tidak berubah, hanya satuan penghitungan dan aturan pembulatan yang berubah.
- Konversi dibagi menjadi “konversi maju” (desimal ke sistem bilangan lain) dan “konversi mundur” (sistem bilangan lain ke desimal), masing-masing memiliki metode perhitungan tetap.
Metode Konversi Sistem Bilangan: Metode Penjumlahan dengan Ekspansi Berbasis Posisi, Metode Pembagian dengan Sisa
- Metode penjumlahan dengan ekspansi berbasis posisi adalah metode untuk konversi dari non-desimal ke desimal
- Metode pembagian dengan sisa adalah metode untuk konversi dari desimal ke non-desimal
Metode Penjumlahan dengan Ekspansi Berbasis Posisi (Non-desimal → Desimal)
Prinsip Inti
Setiap angka dalam sistem bilangan, pada dasarnya adalah jumlah dari “setiap digit × bobot posisi yang sesuai”. Pola bobot adalah: dengan basis sistem bilangan target sebagai dasar, dan urutan posisi (dihitung dari kanan ke kiri, dimulai dari 0) sebagai eksponen. Misalnya, basis bilangan biner adalah 2, bobot posisi ke-1 dari kanan (paling kanan) adalah \(2^0=1\), posisi ke-2 adalah \(2^1=2\), posisi ke-3 adalah \(2^2=4\), dan seterusnya.
Langkah-langkah
- Tentukan setiap digit angka yang akan dikonversi, serta “nilai bobot” posisi yang sesuai (\(nilai\ bobot = basis^{urutan\ posisi}\), urutan posisi dari kanan ke kiri, nilai urutan posisi dimulai dari 0).
- Setiap digit dikalikan dengan nilai bobot yang sesuai, mendapatkan nilai desimal dari posisi tersebut.
- Semua nilai desimal dari setiap posisi dijumlahkan, hasilnya adalah angka desimal akhir.
Contoh
- Biner: \(1001_{(2)} = 1 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 = 8 + 0 + 0 + 1 = 9_{(10)}\)
- Oktal: \(302_{(8)} = 3 \times 8^2 + 0 \times 8^1 + 2 \times 8^0 = 192 + 0 + 2 = 194_{(10)}\)
- Heksadesimal: \(EA7_{(16)} = 14 \times 16^2 + 10 \times 16^1 + 7 \times 16^0 = 3751_{(10)}\)
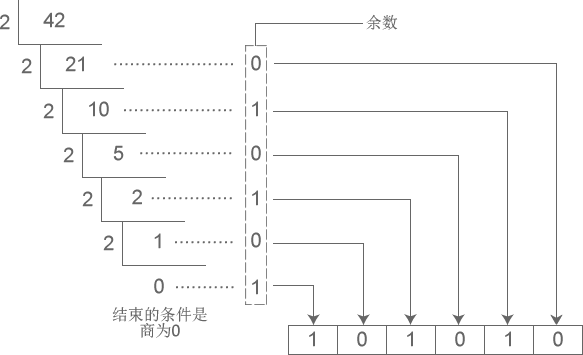
Metode Pembagian dengan Sisa (Desimal → Non-desimal)
Prinsip Inti
Angka desimal dapat dipecah menjadi jumlah dari beberapa pangkat basis sistem bilangan target. Dengan cara “membagi basis dan mengambil sisa”, setiap digit dari posisi terendah ke tertinggi diperoleh secara berurutan, dan akhirnya sisa-sisa diatur secara terbalik. Singkatnya: sisa adalah “posisi rendah”, pembagian lanjutan dari hasil bagi adalah untuk mendapatkan “posisi tinggi”.
Langkah-langkah
- Bagi angka desimal dengan basis sistem bilangan target, mendapatkan hasil bagi dan sisa.
- Gunakan hasil bagi dari langkah sebelumnya untuk terus dibagi dengan basis, ulangi untuk mendapatkan hasil bagi dan sisa baru.
- Hentikan ketika hasil bagi adalah 0, atur semua sisa dalam urutan “yang diperoleh kemudian ditempatkan terlebih dahulu”, yaitu menjadi angka sistem bilangan target.
Contoh
Hubungan antara 17 Bilangan Bulat Desimal Pertama dengan Biner, Oktal, Heksadesimal
| Desimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Biner | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | 10000 |
| Oktal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 20 |
| Heksadesimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 |
Konversi antara Biner dengan Oktal, Heksadesimal
- Konversi biner ke oktal dilakukan dengan pengelompokan 3 bit, ke heksadesimal dengan pengelompokan 4 bit
- Konversi sebaliknya dilakukan dengan pemisahan dan penambahan 0, jika jumlah bit kurang, tambahkan 0 di posisi tinggi hingga cukup.
Biner ke Oktal (2→8)
- Mulai dari ujung kanan angka biner, kelompokkan setiap 3 bit menjadi satu kelompok.
- Jika kelompok paling kiri tidak memiliki 3 bit, tambahkan 0 di depannya untuk mencapai 3 bit.
- Setiap kelompok sesuai dengan satu digit oktal (0-7), kombinasi hasilnya adalah angka oktal.
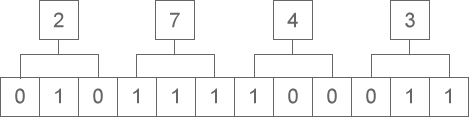
Biner ke Heksadesimal (2→16)
- Mulai dari ujung kanan angka biner, kelompokkan setiap 4 bit menjadi satu kelompok.
- Jika kelompok paling kiri tidak memiliki 4 bit, tambahkan 0 di depannya untuk mencapai 4 bit.
- Setiap kelompok sesuai dengan satu digit heksadesimal (0-9、A-F), kombinasi hasilnya adalah angka heksadesimal.

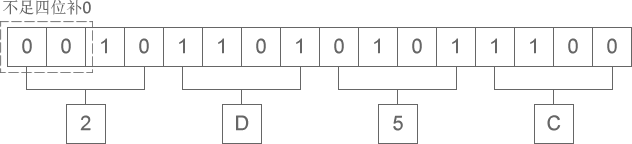
Oktal / Heksadesimal ke Biner (8/16→2)
- Oktal ke biner: Setiap digit oktal, dipecah menjadi 3 bit biner (jika kurang dari 3 bit, tambahkan 0 di depannya).
- Heksadesimal ke biner: Setiap digit heksadesimal, dipecah menjadi 4 bit biner (jika kurang dari 4 bit, tambahkan 0 di depannya).
- Hapus 0 berlebih di paling kiri setelah kombinasi (jika ada), mendapatkan angka biner.
Konversi Sistem Bilangan untuk Bilangan Desimal (Pecahan)
- Desimal→sistem bilangan lain: Bagian bulat menggunakan “pembagian dengan sisa, pengurutan terbalik”, bagian desimal menggunakan “perkalian dengan basis dan pengambilan bulat, pengurutan berurutan”, akhirnya digabungkan.
- Sistem bilangan lain→desimal: Baik bagian bulat maupun bagian desimal menggunakan “penjumlahan dengan ekspansi berbasis posisi”, kemudian hasil digabungkan.
Desimal ke Sistem Bilangan Lain
Bagian Bulat: Pembagian dengan Sisa, Pengurutan Terbalik
- Langkah-langkah: Bagi bilangan bulat desimal dengan basis R, catat sisa; gunakan hasil bagi untuk terus dibagi dengan R, sampai hasil bagi adalah 0; akhirnya atur semua sisa dari belakang ke depan, yaitu bagian bulat sistem R.
- Contoh: Konversi desimal 10 ke biner (R=2)
- \(10 \div 2 = 5\),sisa 0;
- \(5 \div 2 = 2\),sisa 1;
- \(2 \div 2 = 1\),sisa 0;
- \(1 \div 2 = 0\),sisa 1;
- Atur sisa secara terbalik: 1010, yaitu \(10_{(10)} = 1010_{(2)}\).
Bagian Desimal: Perkalian dengan Basis dan Pengambilan Bulat, Pengurutan Berurutan
- Langkah-langkah: Kalikan bilangan desimal (pecahan) dengan basis R, catat bagian bulat (0 atau 1, ketika R=2); gunakan bagian sisa desimal untuk terus dikalikan dengan R, sampai bagian desimal menjadi 0 atau mencapai presisi yang diperlukan; akhirnya atur bagian bulat secara berurutan, yaitu bagian desimal sistem R.
- Contoh: Konversi desimal 0.25 ke biner (R=2)
- \(0.25 \times 2 = 0.5\),bagian bulat 0;
- \(0.5 \times 2 = 1.0\),bagian bulat 1;
- Bagian desimal menjadi 0, hentikan;
- Atur bagian bulat secara berurutan: 01, yaitu \(0.25_{(10)} = 0.01_{(2)}\).
Sistem Bilangan Lain ke Desimal
Bagian Bulat: Bobot adalah \(R^0\)、\(R^1\)、\(R^2\)… (dari kanan ke kiri)
- Langkah-langkah: Kalikan setiap digit dari bilangan bulat sistem R dengan bobot yang sesuai, kemudian jumlahkan.
- Contoh: Konversi biner 1010 ke desimal (R=2)
- Nilai posisi dari kanan ke kiri: Posisi 1 adalah 0 (bobot \(2^0\))、Posisi 2 adalah 1 (bobot \(2^1\))、Posisi 3 adalah 0 (bobot \(2^2\))、Posisi 4 adalah 1 (bobot \(2^3\));
- Perhitungan: \(1\times 2^3 + 0\times 2^2 + 1\times 2^1 + 0\times 2^0 = 8+0+2+0 = 10\).
Bagian Desimal: Bobot adalah \(R^{-1}\)、\(R^{-2}\)、\(R^{-3}\)… (dari kiri ke kanan)
- Langkah-langkah: Kalikan setiap digit dari bilangan desimal (pecahan) sistem R dengan bobot yang sesuai, kemudian jumlahkan.
- Contoh: Konversi biner 0.01 ke desimal (R=2)
- Nilai posisi dari kiri ke kanan: Posisi 1 adalah 0 (bobot \(2^{-1}\))、Posisi 2 adalah 1 (bobot \(2^{-2}\));
- Perhitungan: \(0\times 2^{-1} + 1\times 2^{-2} = 0+0.25 = 0.25\).